Em postagem anterior, analisamos o problema e concluímos que o próximo passo seria resolver a seguinte equação diferencial:


y' = p
y'' = p'
y'' = p'
Substituindo obtemos:
Utilizando a, assim chamada, "notação de Leibniz" para a derivada:
Separando as variáveis:
Integrando ambos os lados:
Pelas regras de integração obtemos:
Pelas propriedades dos logaritmos:
Tomando a exponencial de ambos os lados:
Pelas propriedades básicas das funções exponencias e logarítmicas (e colocando eK = K2):
Desfazendo a última substituição (ou seja, colocando p = y' = y'(z)):
A fim de obter o valor de K1 colocamos z = a nesta última igualdade:
Agora usamos o fato de que y'(a) = 0:
Segue-se da expressão acima que:
Portanto:
Com um pouco de manipulação algébrica podemos escrever y' explicitamente:
![y'+\sqrt{1+[y']^2}=z^ca^{-c}](http://latex.codecogs.com/gif.latex?y'+\sqrt{1+[y']^2}=z^ca^{-c})
![\sqrt{1+[y']^2}=z^ca^{-c}-y'](http://latex.codecogs.com/gif.latex?\sqrt{1+[y']^2}=z^ca^{-c}-y')
![1+[y']^2=\left (z^ca^{-c}-y' \right )^2](http://latex.codecogs.com/gif.latex?1+[y']^2=\left%20(z^ca^{-c}-y'%20\right%20)^2)
![1+[y']^2=z^{2c}a^{-2c}-2z^{c}a^{-c}y'+[y']^2](http://latex.codecogs.com/gif.latex?1+[y']^2=z^{2c}a^{-2c}-2z^{c}a^{-c}y'+[y']^2)
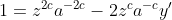
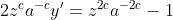
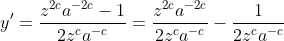
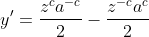
O próximo passo é resolver a equação diferencial acima. Isto faremos na próxima postagem da série.
Referências: na última postagem da série.
O próximo passo é resolver a equação diferencial acima. Isto faremos na próxima postagem da série.
Referências: na última postagem da série.
Relate erros aqui.





.png)












Nenhum comentário :
Postar um comentário